Computer Science/Data Structure
[Data Structure/자료구조][CS] 4. Heap
devYeON_
2022. 4. 3. 23:21
Heap
- 완전 이진트리로 구성된 자료구조
- 여러 값들 중 최솟값과 최댓값을 빠르게 찾는 연산에 최적화된 자료구조
- 느슨한 정렬 상태가 유지됨
- 중복 값을 허용(이진 탐색 트리에선 중복된 값을 허용하지 않음)
🔎 느슨한 정렬이란?
: 완전한 정렬 상태도 아니지만, 정렬이 안되어 있지도 않은 상태
🔎 이진 탐색 트리란?
: 정렬된 이진 트리, 부모 노드보다 작은 값은 왼쪽, 큰 값은 오른쪽으로 정렬(반대 가능), 중복 값 허용 안 함
1. 힙(Heap)의 종류
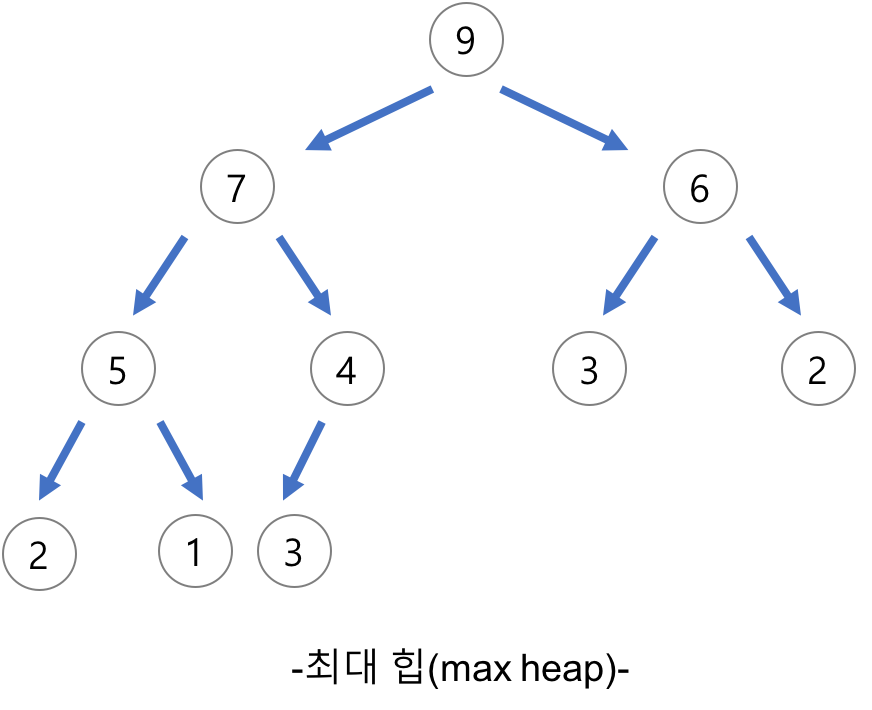
- 최대 힙(Max Heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
- 부모 Node >= 자식 Node
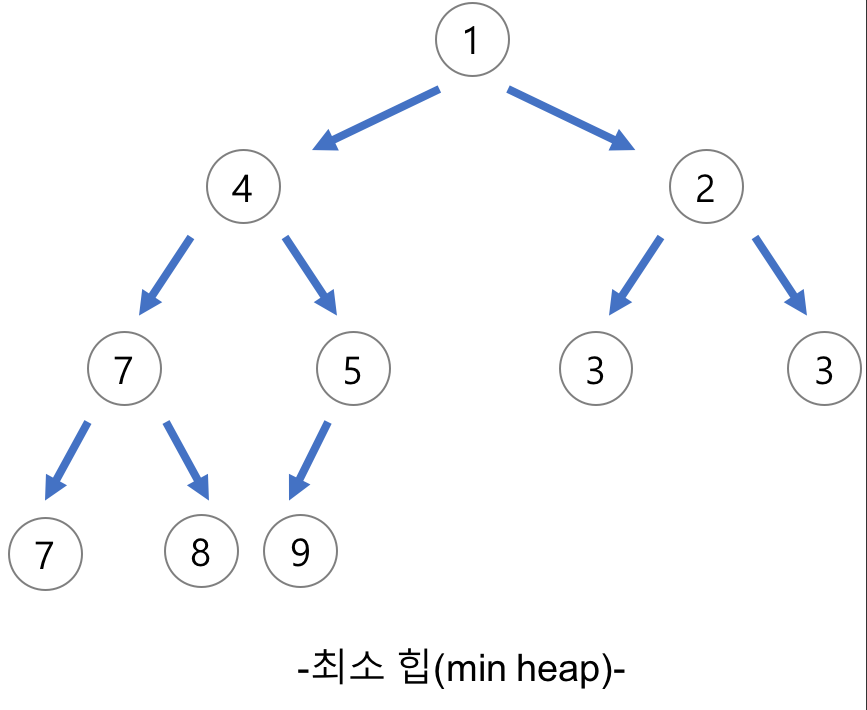
- 최소 힙(Min Heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진트리
- 부모 Node <= 자식 Node
2. 힙(Heap)의 구현
- 배열과 연결 리스트로 구현할 수 있다.
- 배열을 이용하는 것이 연결 리스트보다 실행 속도, 메모리 면에서 효율적이다.
- 연결 리스트로 구현 시 새로운 노드를 ‘마지막 위치’에 추가하는 것이 쉽지 않다.
- 중간에 비어있는 요소가 없기 때문에 배열로 구현이 효율적이다.
- 부모 Node와 자식 Node의 관계
- 왼쪽 자식 Index = 부모 Index * 2
- 오른쪽 자식 Index = (부모 Index * 2) + 1
- 부모 Index = 자식 Index / 2

① Heap 기본 생성 (Max Heap) - ArrayList
class maxHeap {
public static ArrayList<Integer> heap;
public maxHeap() {
heap = new ArrayList<Integer>();
heap.add(0); // 시작 Index를 1로 만들기 위해서 추가
}
public static void main(String[] args) throws Exception {
maxHeap heap = new maxHeap();
heap.insert(3);
heap.insert(7);
heap.insert(2);
heap.insert(4);
heap.insert(6);
heap.insert(8);
heap.insert(1);
heap.insert(9);
heap.insert(10);
System.out.println("End Insert");
System.out.print("Heap: ");
heap.printHeap();
// 출력 결과
// End Insert
// Heap: 10 9 7 8 4 2 1 3 6
System.out.println("Remove Max Value : " + heap.remove());
System.out.print("Heap: ");
heap.printHeap();
// 출력 결과
// Remove Max Value : 10
// Heap: 9 8 7 6 4 2 1 3
}
public void printHeap() throws Exception {
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringBuilder sb = new StringBuilder();
for (int i = 1; i < heap.size(); i++) {
sb.append(heap.get(i)).append(" ");
}
sb.append("\n");
bw.write(sb.toString());
bw.flush();
}
}② 삽입 연산

public void insert(int value) {
heap.add(value); // Heap에 데이터 삽입
int index = heap.size() - 1; // 마지막에 저장된 Index
// Root(1)에 도달할 때 까지 반복
while (index > 1) {
int parentIndex = (index) / 2; // 삽입된 노드의 부모 인덱스
// 현재 노드의 값이 부모의 값보다 크다면
if (heap.get(index) > heap.get(parentIndex)) {
// 부모와 노드 위치 Swap
int temp = heap.get(index);
heap.set(index, heap.get(parentIndex));
heap.set(parentIndex, temp);
// 현재 노드 인덱스 갱신
index = parentIndex;
}
else {
// 부모 노드의 값이 더 크면 반복문 종료
break;
}
}
}③ 삭제 연산
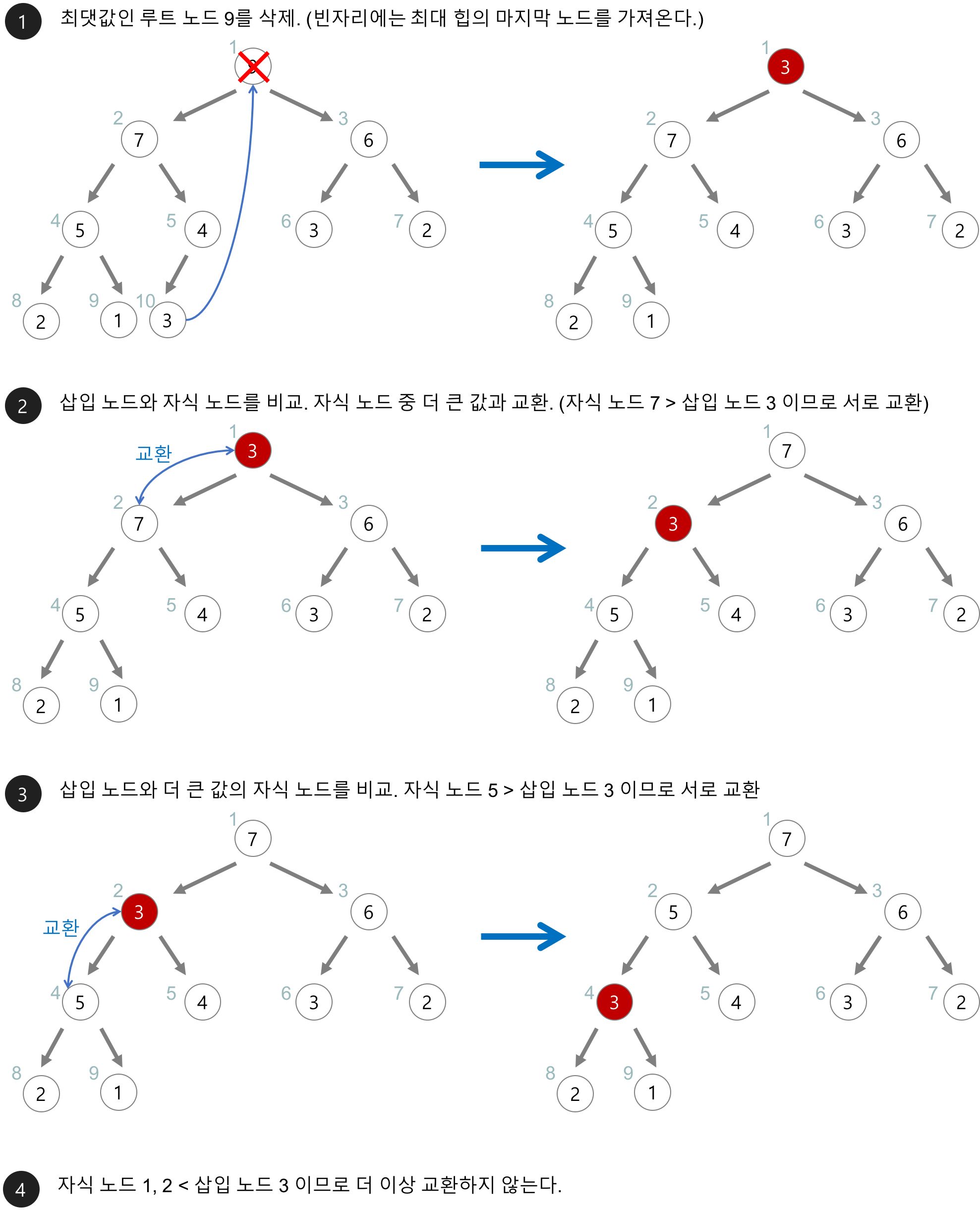
public int remove() {
int max = heap.get(1); // Root Node의 값 저장
int last = heap.remove(heap.size() - 1); // 마지막 Node 값 저장
if (heap.size() > 1) { // Heap이 비어있지 않은 경우
heap.set(1, last); // Root Node를 마지막 Node 값 변경
int index = 1; // Root Node Index
int left = 2 * index; // // 왼쪽 자식 Node Index
int right = 2 * index + 1; // 오른쪽 자식 Node Index
// 왼쪽 오른쪽 자식이 모두 존재 할 때
while (left < heap.size() && right < heap.size()) {
// 왼쪽 Index의 값이 오른쪽 Index 값보다 크다면,
if (heap.get(left) > heap.get(right)) {
// 왼쪽 자식의 값이 현재 값보다 크다면 Swap
if (heap.get(left) > heap.get(index)) {
int temp = heap.get(left);
heap.set(left, heap.get(index));
heap.set(index, temp);
// 현재 Index 갱신
index = left;
}
else {
// 현재 값이 왼쪽 자식의 값보다 크다면 종료
break;
}
}
// 오른쪽 Index값이 왼쪽 Index 값보다 크다면
else {
// 오른쪽 자식의 값이 현재 값보다 크다면 Swap
if (heap.get(right) > heap.get(index)) {
int temp = heap.get(right);
heap.set(right, heap.get(index));
heap.set(index, temp);
index = right;
} else {
break;
}
}
// 현재 Index가 바뀌었기 때문에 자식 Index도 갱신
left = 2 * index;
right = 2 * index + 1;
}
}
// 기존의 Root 노드 값 반환.
return max;
}④ Priority Queue로 구현
public class Priority_maxHeap {
public static void main(String[] args) throws Exception {
// 우선순위 큐(Priority Queue) 선언 <MaxHeap>
PriorityQueue<Integer> pq = new PriorityQueue<Integer>(Collections.reverseOrder());
// 우선순위 큐(Priority Queue) 선언 <MinHeap>
// PriorityQueue<Integer> pq = new PriorityQueue<Integer>();
// 데이터 추가
pq.add(3);
pq.add(7);
pq.add(2);
pq.add(4);
pq.add(6);
pq.add(8);
pq.add(1);
pq.add(9);
pq.add(10);
pq.add(5);
// 우선순위 큐(Priority Queue) 출력
print(pq);
// poll() : 우선순위 큐(Priority Queue)의 최대값을 삭제하고 반환한다.
// remove() : 우선순위 큐(Priority Queue)의 최대값을 삭제하고 반환하지 않는다.
// pq.poll();
pq.remove();
// 우선순위 큐(Priority Queue) 출력
print(pq);
}
public static void print(PriorityQueue<Integer> pq) throws Exception {
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringBuilder sb = new StringBuilder();
// 우선순위 큐(Priority Queue)의 요소들을 순서대로 출력한다.
Iterator it = pq.iterator();
while (it.hasNext()) {
sb.append(it.next() + " ");
}
sb.append("\n");
bw.write(sb.toString());
bw.flush();
}
}
3. Heap의 정렬
- n개의 요소는 $O(nlog_2n)$시간 안에 정렬됨. → 요소의 개수가 n개이고 하나의 요소를 heap에 삽입, 삭제할 경우 heap 재정비하는 시간이 $log_2n$만큼 소요되기 때문에 전체적으로 $O(nlog_2n)$이 소요
- 가장 큰 값 몇 개만 필요할 때 사용, 간단한 정렬 알고리즘이 $O(n^2)$이기에 전체 자료를 정렬하기에는 시간이 많이 소요됨.
- 내림차순 정렬을 위해서는 최대 힙을 구성, 오름차순 정렬을 위해서는 최소 힙을 구성
- 과정
- 정렬해야 할 n개의 요소들로 최대 힙(완전 이진트리 형태)을 만든다. → 내림차순 기준으로 정렬
- 한 번에 하나씩 요소를 heap에서 꺼내 배열의 맨 뒤부터 저장
- 삭제되는 요소들(최댓값부터 삭제)은 값이 감소되는 순서로 정렬되게 된다.
- 정렬 코드
import java.util.PriorityQueue;
public class test {
public static void main(String[] args) {
int[] arr = {3, 7, 5, 4, 2, 8};
System.out.print(" 정렬 전 original 배열 : ");
for(int val : arr) {
System.out.print(val + " ");
}
PriorityQueue<Integer> heap = new PriorityQueue<Integer>();
// 배열을 힙으로 만든다.
for(int i = 0; i < arr.length; i++) {
heap.add(arr[i]);
}
// 힙에서 우선순위가 가장 높은 원소(root노드)를 하나씩 뽑는다.
for(int i = 0; i < arr.length; i++) {
arr[i] = heap.poll();
}
System.out.print("\n 정렬 후 배열 : ");
for(int val : arr) {
System.out.print(val + " ");
}
}
}
4. 정렬 알고리즘 시간 복잡도
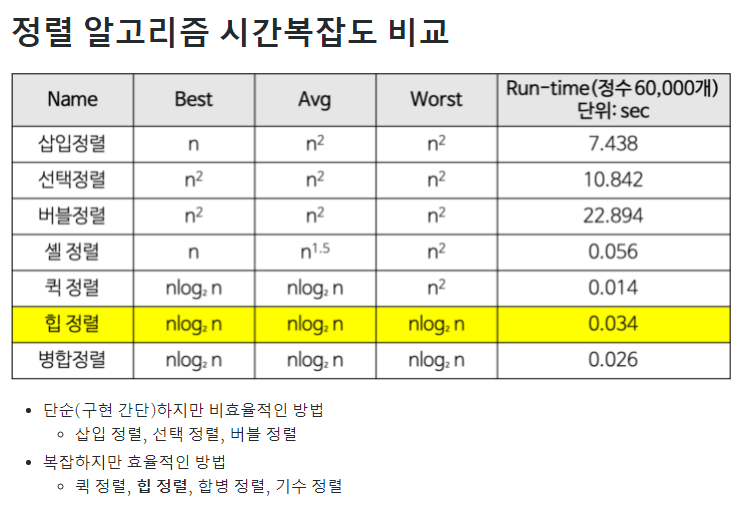
CS 스터디 팀원의 자료조사를 기반으로 작성하였습니다 🤗🤗